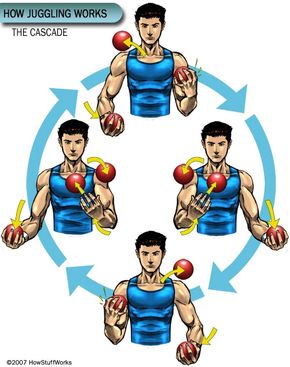
The cascade provides the basis for hundreds of three-ball juggling tricks and variations. The most common variation is the reverse cascade. In a reverse cascade, ascending balls go over the arcs of the descending balls instead of under them. Your hands move in the opposite direction they would for a normal cascade -- counterclockwise for your right hand and clockwise for your left. In other words, instead of scooping your hands inward, you scoop them outward. Most new jugglers find the pattern a little more challenging and less natural than the basic cascade.
Another variation is the half shower. In a half shower, the juggler tosses the balls from one hand in a reverse cascade pattern (scooping outwards) and uses a regular cascade pattern with the other hand (scooping inwards). The pattern can go clockwise or counterclockwise, and, it's quite easy to shift from one to the other with a little practice.
Tennis is another variation that is between the reverse cascade and the normal cascade. In tennis, the juggler tosses one ball in a reverse cascade while tossing the other two balls in a regular cascade pattern. The ball in the reverse cascade passes over the other two balls, much like a ball over the net in a tennis match.
The shower is one of the more difficult basic variations. A shower pattern is circular -- one hand throws the balls in an arc while the other catches and feeds them back to the first hand. Some jugglers use a very low, fast toss from the catching hand to the tossing hand, while others actually put the ball into the tossing hand. Most people naturally gravitate to this pattern when practicing with two balls, but once you get up to three it becomes pretty challenging.
Other variations require the juggler to cross his arms and make throws under the other arm. Doing this once is simple, but there are complex patterns that require jugglers to constantly cross and uncross their arms while keeping a juggling pattern going. One such pattern is called Mills Mess, invented by Steve Mills. In this pattern, the juggler's arms do all the crossing -- the balls actually never cross paths at all. There are many other variations of three-ball routines with equally interesting names. Burke's Barrage and Rubenstein's Revenge are two other well-known variations.
You can even juggle balls upside down. Bounce juggling is just what it sounds like. Instead of tossing balls up into the air, you bounce them against the ground and catch them on the rebound. Jugglers can use a lift bounce by lightly tossing each ball upward and letting it fall to the ground, or they can use a force bounce by throwing the ball at the ground. Force bouncing is faster but gives jugglers more control and accuracy.
Common tricks with three-ball juggling include tossing balls behind the back or under the leg as well as bouncing a ball off a body part like the knee, foot or forehead. You might also see a juggler catch objects using a fast, downward grabbing motion, called clawing. Or, he might move an object in a fast, diagonal slash across the pattern and toss it under his other arm, which is called a chop. Other old standbys include juggling an apple and taking the occasional bite or making a face by holding one ball in the mouth and the other two over the eyes. Many modern jugglers look on these tricks with contempt, feeling that tricks such as these keep juggling in the realm of the sideshow. To see examples of these variations, please refer to the video on the first page of the article.