If you've been in a book store in the last six months -- or an airport, waiting room or college lecture class -- you've probably seen someone staring at a sudoku. Given its popularity, one might think it's some new type of porn. But no, it's just a puzzle. It's a widespread, logic-based fad of a puzzle that is simple enough to suck you in and difficult enough to keep you hooked.
In this article, we'll find out what a sudoku puzzle entails, how to go about solving one and where the concept originated (hint: It's not Japan. Let's get started.
Advertisement
Sudoku Basics
Sudoku (or su doku) is a game of numbers -- specifically, the numbers 1 through 9 -- but it really isn't about math. It's about logic. Instead of 1 through 9, you could use the first nine letters of the alphabet or a set of nine symbols, and it would be the same game.
The basis of the sudoku game is a nine-by-nine grid. You've got three sections to think about: rows, columns and boxes.
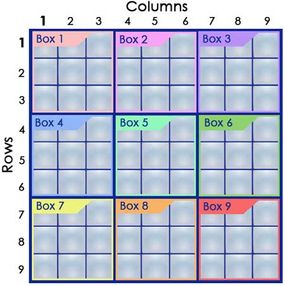
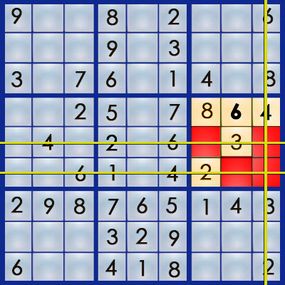
The goal of sudoku is to fill each nine-square row, each nine-square column and each nine-square box with the numbers 1 through 9, with each number used once and only once in each section. It's the interaction between the rows, columns and boxes that tells you where the numbers need to go. So if you were to start with a blank grid and fill in the numbers for row 1, column 2 and box 4 according to the sudoku rules, it might look something like this:
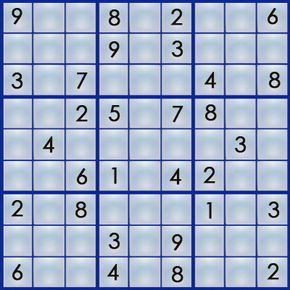
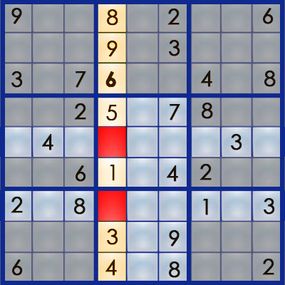
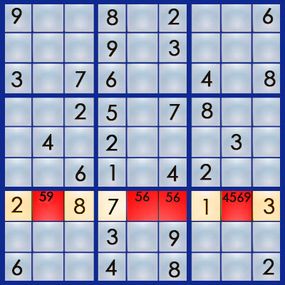
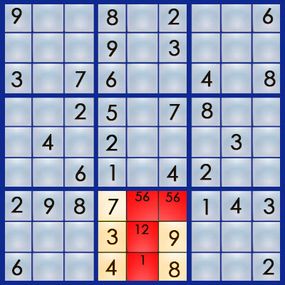
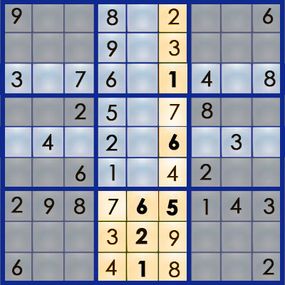
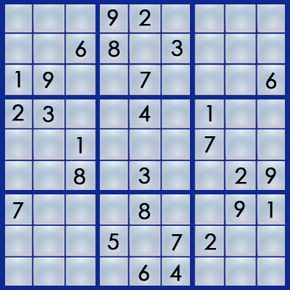
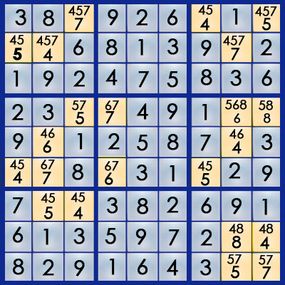
Of course, starting with a blank grid wouldn't make it much of a challenge. A sudoku puzzle already has some of the numbers filled in, and it's your job to figure out where the rest of the numbers go. Here's an example of a real sudoku puzzle from Michael Mepham's "Book of Sudoku 3":

Sudoku has several levels of difficulty, from easy to very hard, based on how many numbers you get to start with and where those numbers are positioned. (Michael Mepham, puzzle creator for London's Daily Telegraph, rates his puzzles as either Gentle, Moderate, Tough or Diabolical.) An easy puzzle gives you enough numbers placed in enough strategic positions to allow you to find the answer using fairly simple logic. Each puzzle has only one answer.
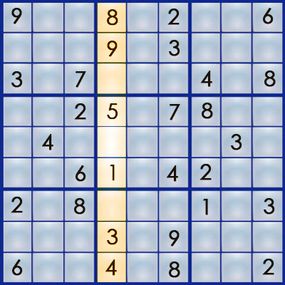
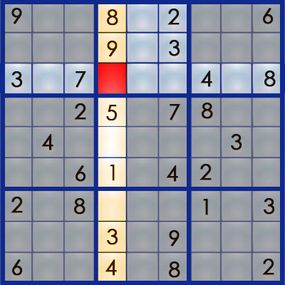
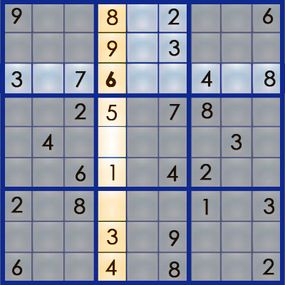
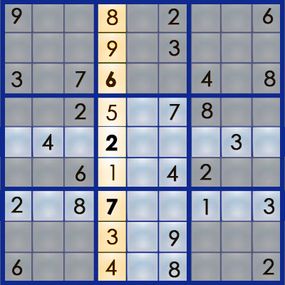
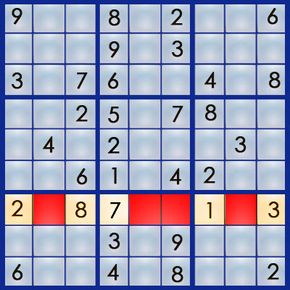
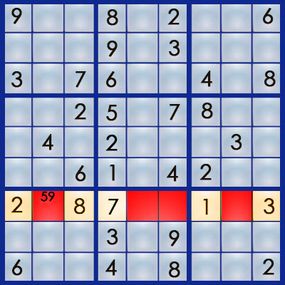
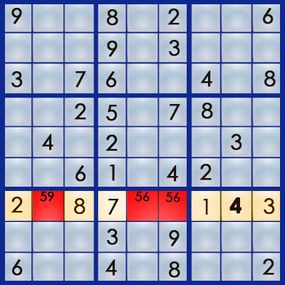
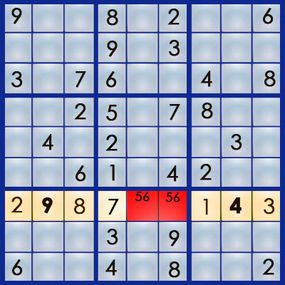
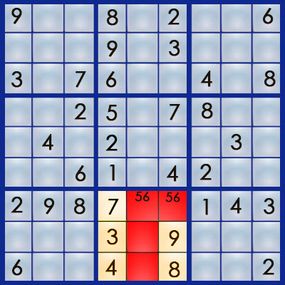
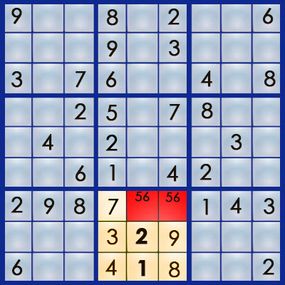
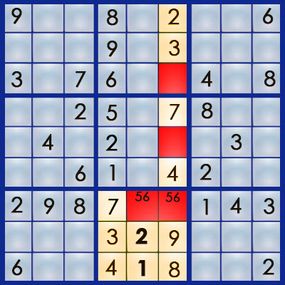
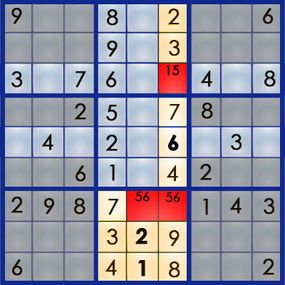
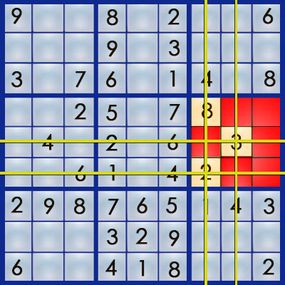
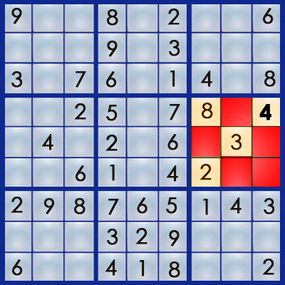
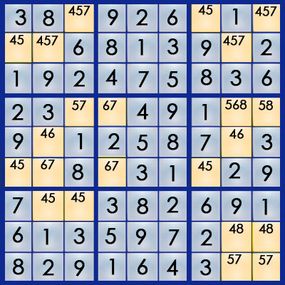
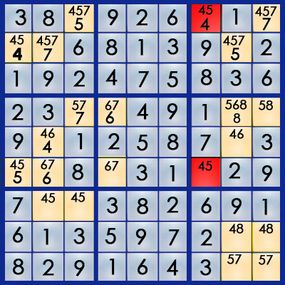
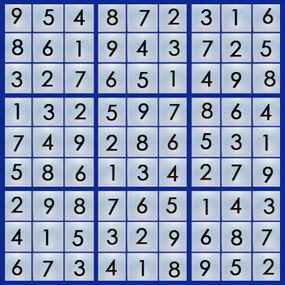
The best way to learn the art of sudoku is by working through a puzzle. Let's walk our way through the easy puzzle above to get a feel for the process. If you can solve an easy puzzle, you can solve a hard one -- it'll just take you more time.
Advertisement