If you have ever compared an electric guitar to an acoustic guitar, you know that they have several important things in common. Both acoustic and electric guitars have six strings, they both tune those strings with tuning pegs and they both have frets on a long neck. Down at the body end is where the major differences are found.
Electric guitars have solid bodies, magnetic pickups and several knobs instead of the hollow resonating cavity found in an acoustic guitar. If you pluck a string on an electric guitar that is not plugged in, the sound is barely audible. Without a soundboard and a hollow body, there is nothing to amplify the string's vibrations.
Advertisement
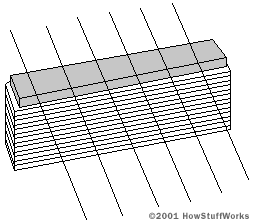
To produce sound, an electric guitar senses the vibrations of the strings electronically and routes that electronic signal to an amplifier and speaker. The sensing occurs in a magnetic pickup mounted under the strings on the guitar's body. A simple magnetic pickup looks like this:
This pickup consists of a bar magnet wrapped with perhaps 7,000 turns of fine wire. If you have read How Electromagnets Work, then you know that coils and magnets can turn electrical energy into motion. In the same way, they can turn motion into electrical energy. In the case of an electric guitar, the vibrating steel strings produce a corresponding vibration in the magnet's magnetic field and therefore a vibrating current in the coil.
There are many different types of pickups. For example, many pickups use a separate magnet for each string, like this:
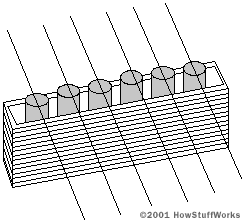
Separate magnets allow the guitarist to adjust the height of each magnet independently of the others.
The coil sends its signals through a very simple circuit on most guitars. The circuit looks something like this:
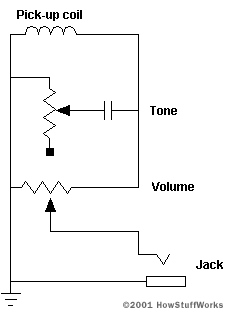
The upper variable resistor adjusts the tone. The resistor (500 kilo-ohms max) and capacitor (0.02 microfarads) form a simple low-pass filter. The filter cuts out higher frequencies. By adjusting the resistor, you control the frequencies that are cut out. The second resistor (500 kilo-ohms max) controls the amplitude (volume) of the signal that reaches the jack. The signal runs from the jack to an amplifier, which drives a speaker.
Many electric guitars have two or three different pickups located at different points on the body. Each pickup has a distinctive sound, and multiple pickups can be paired, either in-phase or out, to produce additional variations.
Here are some interesting links:
Advertisement