How the Physics of Football Works

When the football travels through the air, it always follows a curved, or parabolic, path because the movement of the ball in the vertical direction is influenced by the force of gravity. As the ball travels up, gravity slows it down until it stops briefly at its peak height; the ball then comes down, and gravity accelerates it until it hits the ground. This is the path of any object that is launched or thrown (football, arrow, ballistic missile) and is called projectile motion. To learn about projectile motion as it applies to football, let's examine a punt (Figure 1). When a punter kicks a football, he can control three factors:

The rotation of the ball -- spiral or end-over-end -- will influence how the ball slows down in flight, because the ball is affected by air drag. A spiraling kick will have less air drag, will not slow down as much and will be able to stay in the air longer and go farther than an end-over-end kick. The velocity of the ball and the angle of the kick are the major factors that determine:

When the ball leaves the punter's foot, it is moving with a given velocity (speed plus angle of direction) depending upon the force with which he kicks the ball. The ball moves in two directions, horizontally and vertically. Because the ball was launched at an angle, the velocity is divided into two pieces: a horizontal component and a vertical component. How fast the ball goes in the horizontal direction and how fast the ball goes in the vertical direction depend upon the angle of the kick. If the ball is kicked at a steep angle, then it will have more velocity in the vertical direction than in the horizontal direction -- the ball will go high, have a long hang-time, but travel a short distance. But if the ball is kicked at a shallow angle, it will have more velocity in the horizontal direction than in the vertical direction -- the ball will not go very high, will have a short hang-time, but will travel a far distance. The punter must decide on the best angle in view of his field position. These same factors influence a pass or field goal. However, a field goal kicker has a more difficult job because the ball often reaches its peak height before it reaches the uprights.

If you are not interested in the details of calculating the hang-time, peak height and range of a punt, click here to skip the following page.

The parabolic path of a football can be described by these two equations:

y = Vyt - 0.5gt2

y = V_yt - 0.5gt²

x =Vxt

x =V_xt

To calculate the hang-time (t_total), peak height (y_max), and maximum range (x_max) of a punt, you must know the initial velocity (V) of the ball off the kicker's foot, and the angle (theta) of the kick.

The velocity must be broken into horizontal (V_x) and vertical (V_y) components according to the following formulas: 

The hang-time (t_total) must be determined by one of these two formulas:

Once you know the hang-time, you can calculate maximum range (x_max):

You can calculate the time (t_1/2) at which the ball is at its peak height:

And you can calculate the peak height (y_max), using one of these two formulas: 

For example, a kick with a velocity of 90 ft/s (27.4 m/s) at an angle of 30 degrees will have the following values:

Vertical and horizontal components of velocity:

Hang-time:

Maximum range:

Time at peak height:

Peak height:

If we do the calculations for a punt with the same velocity, but an angle of 45 degrees, then we get a hang-time of 3.96 s, a maximum range of 76.8 m (84 yd), and a peak height of 36.5 m (120 ft). If we change the angle of the kick to 60 degrees, we get a hang-time of 4.84 s, a maximum range of 66.3 m (72 yd), and a peak height of 54.5 m (179 ft). Notice that as the angle of the kick gets steeper, the ball hangs longer in the air and goes higher. Also, as the angle of the kick is increased, the distance traveled by the ball increases to a maximum (achieved at 45 degrees) and then decreases.

When we look at runners on the field, several aspects can be considered:

Line-Up Positions

When we look at the positions of the backs, both offensive and defensive, we see that they typically line up away from the line of scrimmage on either side of the offensive and defensive linemen. Their positioning allows them room, or time, to accelerate from a state of rest and reach a high speed, to either run with the ball or pursue the ball carrier. Notice that the linebackers have far more room to accelerate than the linemen, and the wide receivers have far more room than the linebackers. So linebackers can reach higher speeds than linemen, and wide receivers can reach the highest speeds of all.

Changing Directions on the Field

Let's look at an example of a running play in which the quarterback hands the ball off to a running back. First, the running back starts from the set position, at rest, and accelerates to full speed (22 mi/h or 9.8 m/s) in 2 s after receiving the ball. His acceleration (a) is:

a = (vf - vo)/(tf - to)

a = (v_f - v_o)/(t_f - t_o)

a=(9.8 m/s - 0 m/s)/(2 s - 0 s)

a= 4.9 m/s²

As he runs with the flow of the play (e.g. to the right), he maintains constant speed (a = 0). When he sees an opening in the line, he plants his foot to stop his motion to the right, changes direction and accelerates upfield into the open. By planting his foot, he applies force to the turf. The force he applies to the turf helps to accomplish two things:

To stop his motion to the right, two forces work together. First, there is the force that he himself applies to the turf when he plants his foot. The second force is the friction between his foot and the turf. Friction is an extremely important factor in runners changing direction. If you have ever seen a football game played in the rain, you have seen what happens to runners when there is little friction to utilize. The following is what happens when a runner tries to change his direction of motion on a wet surface:

The applied force and the frictional force together must stop the motion to the right. Let's assume that he stops in 0.5 s. His acceleration must be:

*The negative sign indicates that the runner is accelerating is in the opposite direction, to the left.

The force (F) required to stop him is the product of his mass (m), estimated at 98 kg (220 lbs), and his acceleration:

To accelerate upfield, he pushes against the turf and the turf applies an equal and opposite force on him, thereby propelling him upfield. This is an example of Isaac Newton's third law of motion, which states that "for every action there is an equal, but opposite reaction." Again, if he accelerates to full speed in 0.5 s, then the turf applies 1921 N, or about 500 lbs, of force. If no one opposes his motion upfield, he will reach and maintain maximum speed until he either scores or is tackled.

Running in an Open Field

When running in an open field, the player can reach his maximum momentum. Because momentum is the product of mass and velocity, it is possible for players of different masses to have the same momentum. For example, our running back would have the following momentum (p):

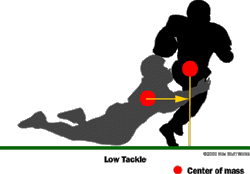
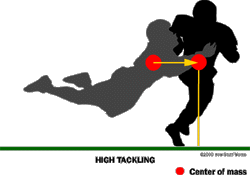
For a 125 kg (275 lb) lineman to have the same momentum, he would have to move with a speed of 7.7 m/s. Momentum is important for stopping (tackling, blocking) runners on the field.

Tackling and blocking runners relies on three important principles of physics:

When Runner and Tackler Meet

When our running back is moving in the open field, he has a momentum of 960 kg-m/s. To stop him -- change his momentum -- a tackler must apply an impulse in the opposite direction. Impulse is the product of the applied force and the time over which that force is applied. Because impulse is a product like momentum, the same impulse can be applied if one varies either the force of impact or the time of contact. If a defensive back wanted to tackle our running back, he would have to apply an impulse of 960 kg-m/s. If the tackle occurred in 0.5 s, the force applied would be:

F = impulse/t = (960 kg-m/s)/(0.5 s) = 1921 N = 423 lb

Alternatively, if the defensive back increased the time in contact with the running back, he could use less force to stop him.

In any collision or tackle in which there is no force other than that created by the collision itself, the total momentum of those involved must be the same before and after the collision -- this is the conservation of momentum. Let's look at three cases:

For the discussion, we will consider an elastic collision, in which the players do not remain in contact after they collide.

In many instances, tacklers try to hold on to the ball carrier, and the two may travel together. In these inelastic collisions, the general reactions would be the same as those above; however, in cases 2 and 3, the speeds at which the combined players would move forward or backward would be reduced. This reduction in speed is due to the fact that the difference in momentum is now distributed over the combined mass of the two players, instead of the mass of the one player with the lesser momentum.

Coaches often tell their players to tackle a runner low. In this way, the runner's feet will be rotated in the air in the direction of the tackle. Let's look at this closely:

Imagine that the runner's mass is concentrated in a point called the center of mass. In men, the center of mass is located at or slightly above the navel; women tend to have their center of mass below their navels, closer to their hips. All bodies will rotate easiest about their center of mass. So, if a force is applied on either side of the center of mass, the object will rotate. This rotational force is called torque, and is the product of the amount of force applied and the distance from the center of mass at which the force applied. Because torque is a product, the same torque can be applied to an object at different distances from the center of mass by changing the amount of force applied: Less force is required farther out from the center of mass than closer in. So, by tackling a runner low -- far from the center of mass -- it takes less force to tackle him than if he were tackled high. Furthermore, if a runner is hit exactly at his center of mass, he will not rotate, but instead will be driven in the direction of the tackle.

Similarly, coaches often advise linemen to stay low. This brings their center of mass closer to the ground, so an opposing player, no matter how low he goes, can only contact them near their center of mass. This makes it difficult for an opposing player to move them, as they will not rotate upon contact. This technique is critical for a defensive lineman in defending his own goal in the "red" zone, the last 10 yards before the goal line.

We have only touched on some of the applications of physics as they relate to football. Remember, this knowledge appears to be instinctive; Most often, players and coaches don't consciously translate the mechanics of physics into their playing of the sport. But by making that translation, we can understand and appreciate even more just how amazing some of the physical feats on the football field really are. Also, applying physics to football leads to better and safer equipment, affects the rules of the sport, improves athletic performance, and enhances our connection to the game.

For more information on football physics and related topics, check out the links on the next page.