Depending on what circles you run in -- say, your best friend is a computer programmer and your sister is a chess prodigy -- you may already be familiar with the 8 Queens puzzle. For the rest of us, the 8 Queens puzzle (or problem or simply "8 Queens") is probably not something we spend a lot of our time thinking about.
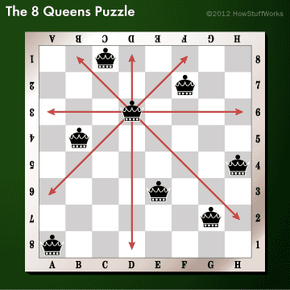
The puzzle is simple enough. How can you place 8 queens on a chessboard so that no two attack each other? Alternately, the question is sometimes stated as "What is the maximum number of queens that can be placed on a chessboard, so that no two can attack each other," but this puzzle becomes a lot less hard when you Google that, and the term "the 8 Queens puzzle" comes up.
Advertisement
You might be asking yourself why on Earth anyone cares where you keep your eight queens. And yes, superficially, it is just a strategic puzzle. But (and this is where it's handy to have a best friend who codes computers) the 8 Queens puzzle is a great way to test the savvy and literacy of a programmer.
Now, don't be scared. You will not be forced to understand the intricacies of computer programming in order to keep reading. But you should know that solving the puzzle can be achieved using a programming code -- and some are more elegant than others. For instance, you can definitely find the solution using a "brute-force" program that might simply go through every possible placement, ruling out one at a time. But a sophisticated coder will be able to construct a program that has shortcuts using a more refined algorithm to find you a solution faster. Being able to come up with unusual or original ways to code a solution to a problem as broad as 8 Queens can be a great test for the savvy of a code-writer.
So while we won't be stringing 1s and 0s at you to explain how 8 Queens works, we will be giving you a few solutions to the puzzle.
Advertisement